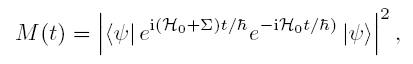
The study of the Loscmidt Echo started in 1995 with NMR experiments in many-body spin systems [1]. There, a hipersensitivity of time reversal to perturbations was found, along with a characteristic decoherence time roughly independent of the perturbation. In these experiments, quantum irreversibility is monitored through the attenuation of the amount of revival of a local density excitation upon time reversal of its quantum evolution, i.e. the Loschmidt Echo. Its mathematical expression is quite simple,
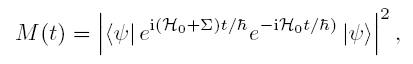
Where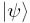 
is an initial state of the system, 
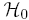its Hamiltonian, and 
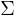the
perturbation. The first attempt to explain the experimental results used that such a complex many-body system could be assumed to be chaotic. This was
reinforced by the fact that the decoherence time was found to be proportional to the only dynamical scale of the system. Using analytical semiclassical
theory, Jalabert and Pastawski [2] predicted that if time reversal were attempted in a classically chaotic system, when a quenched disorder perturbation is
present, the Loschmid Echo would attenuate exponentially. Notably, its decay rate is only determined by the Lyapunov exponent of the classical system. A
bunch of numerical has come out since then. Using different systems, methods and perturbations, we are exploring the limits of the theory (parameter ranges,
soft chaos, etc). The main results have been obtained in the Lorentz Gas, the Bunimovich Stadium and the Smooth Billiard, all standard examples of classical
chaos. Some nice pictures are available in this page, but for the serious work see references.
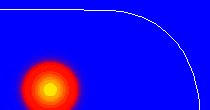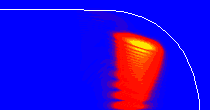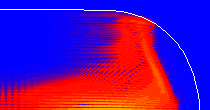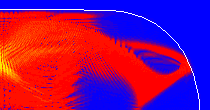
We consider a particle in a square billiard of area L2 where we place an irregular array of N circular scatterers of radius R.
| (a) |  |
(b) |  |
| (c) |  |
(d) |  |
(a) A particular realization of such system, where the length, in a minimal unit a, is L=200a. In the center of the figure is the density of the initial Gaussian wave packet.
(b) The density resulting from the evolution of the initial state in (a), where the initial momentum points to the left. The propagation time is
.
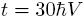(c) An evolution for an equivalent time, but with the perturbed Hamiltonian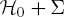 
.
(d) Evolution for time 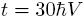with Hamiltonian 
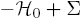of the state depicted in panel (b).
While the densities in panels (b) and (c) look similar to the eye, the corresponding square of the overlap, M(t), between both evolutions is
about 0.09 indicating the relevant role of the quantum phase. Here are the animated sequences of the system shown above, with the Forward
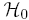and Backward 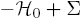evolution (zoomed for convenience).
As stated above, another system where the Loschmidt Echo is being investigated is the Smooth Billiard, which is defined by the potential
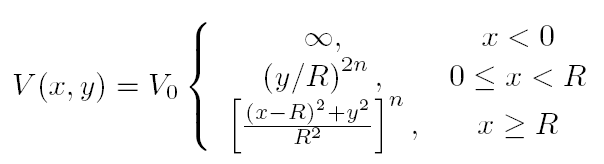
The exponent n sets the steepness of the confining potential. For n=1 the smooth stadium is integrable. As the value of n is increased, the borders become steeper. In the limit of n->infinity, the stadium gains hard walls, becoming the well-know Bunimovich billiard. Thus, by varying n, we can tune the system dynamics from integrable to progressively more chaotic and study the behavior of the Loschmidt Echo in this situations. A little animation showing the evolution of a wave packet in this system is below.
The study of the Loschmidt Echo is an ongoing international collaboration with people from Latin-America and Europe. Up to now, the people involved are the following:
[1] P.R. Levstein, G. Usaj and H.M. Pastawski, J. Chem. Phys. 108, 2718 (1998); G. Usaj, H.M. Pastawski and P.R. Levstein, Mol. Phys.95, 1229 (1998); H.M. Pastawski, P.R. Levstein, G. Usaj, J. Raya and J. Hirschinger, Physica A 283, 166 (2000).
[2] R. Jalabert and H.M. Pastawski, Phys. Rev. Lett. 86, 2490 (2001).
[3] F. M. Cucchietti, H.M. Pastawski and D.A. Wisniacki, Phys. Rev. E 65, 045206(R) (2002).
Article in "The economist", Echoes of the Future
Article in "La voz del Interior", El maquinista del tiempo
Original site design: Fernando M. Cucchietti
Contact: Dr. Horacio M. Pastawski